The theory of quantum chaos is elusive to characterize. In classical chaos, a chaotic dynamics suffer high sensitivity to initial condition. A phenomenon known as butterfly effect. In quantum unitary dynamics, different initial states cannot lead to an exponential separation of trajectories, as a trivial consequence of the conservation of the inner product between states. A quantum version of the butterfly effect means that the chaotic unitary dynamics spread the operator throughout the systems in a way that measuring a local operator has a non-trivial effect on the measurement of a spatially separated local operator. This corresponds to the decay of the Out-of-Time-Order Correlation functions (OTOCs), whose general expression is:
\[OTOC_{2k}(U)=\frac{1}{d}\operatorname{tr}(A_1(U)B_1A_2(U)B_2\cdots A_{k}(U)B_{k})\]
where \(A(U)=U^{\dagger}AU\) is the unitary evolution of a traceless Hermitian operator \(A\).
Waiting for a more satisfactory definition of quantum chaos, we define a unitary operator U to be chaotic if it attains a Haar value for general multi-point
\(2k\) OTOCs, i.e. the value that would be reached by a generic unitary operator. This definition helps to relate the concept of chaos to the one of quantum pseudorandomness: a set of unitary operators, say \(\mathcal{E}\), is a unitary \(k\)-design iff it reproduces the value of \(2k\)-point OTOCs. While a \(k\)-design is automatically a \(k^\prime\)-design for any \(k^\prime<k\), being a \(k+1\)-design is not garanteed. This is the case of the Clifford group: it is a unitary \(3\)-design, but fails to be a unitary \(4\)-design. Physically this means that Clifford unitary operators are able to create highly entangled states - a peculiar example is the Bell state - but, at the same time, the produced entanglement does not display complex features. For example, unlike random states, states entangled by means of Clifford gates can be efficiently disentangled. It is also well-known that Clifford circuits are efficiently simulable by classical resources, and the simulation cost increases exponentially in the number of non-Clifford gates injected in the circuit. This facts raise the question of whether, by doping Clifford circuit with non-Clifford gates, it is possible to reproduce the value of higher order OTOCs, and thus to simulate quantum chaotic evolutions. Below, the general form a \(t\)-doped Clifford circuit:
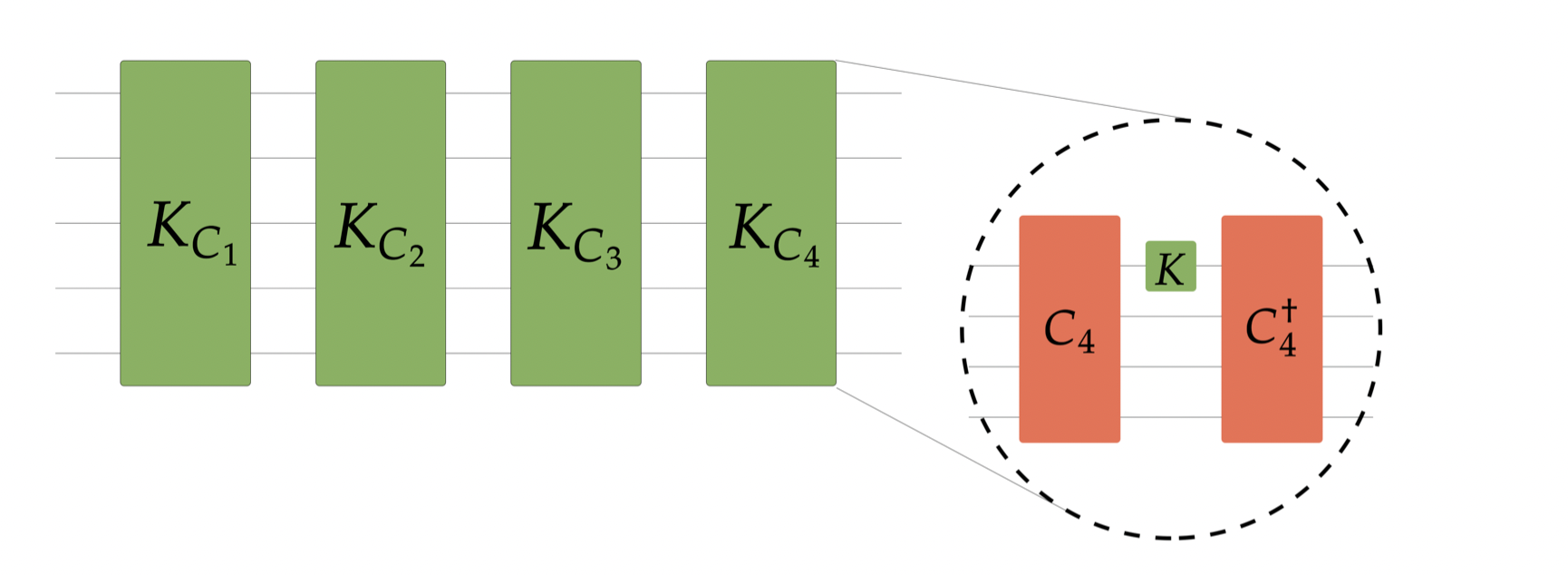
While to form a \(\epsilon\)-approximate unitary design is sufficient to dope Clifford circuits with a vanishing density \(t/n\) of non-Clifford gates, the task of reproducing higher order OTOCs requires much more resources…
In Quantum chaos is quantum, we proved that, to simulate quantum chaos, \((i)\) the accuracy \(\epsilon\) must be exponentially small in \(n\) , and \((ii)\) \(O(n)\) non-Clifford resources are necessary and sufficient to reproduce the value of the \(2k\)-order OTOCs.
\[\text{Haar} \quad OTOC_8(U)= \frac{1}{d^4}\]
\[\text{Clifford} \quad OTOC_8(C)= \frac{1}{d^2}\]
\[t-\text{doped Clifford} \quad OTOC_8(U_t)= \frac{(3/4)^t}{d^2}\]
As a by-product, the above results reflect the impossibility to simulate quantum chaos by classical resources: the simulation is indeed exponentially hard in \(n\), while requing only \(O(poly(n))\) quantum gates. Quantum chaos can only be simulated quantum-mechanically.
The quantum simulation of quantum chaotic evolution can be done either \((i)\) by doping Clifford circuits with non-Clifford gates, e.g. the \(P_{\theta}\)-gate
\[P_{\theta}=\begin{pmatrix}
1 &0 \\
0 & e^{i\theta}
\end{pmatrix}\]
or \((ii)\) by single qubit projective measurement in a non-Clifford basis, the magic state basis:
\[|P_{\theta}\rangle=|0\rangle + e^{i\theta}|1\rangle\]
We indeed investigated such option in Transition in entanglement complexity in random quantum circuit by measurements finding that \(O(n)\) measurements are necessary and sufficient to create states whose entanglement is complex enough to resemble chaotic features.
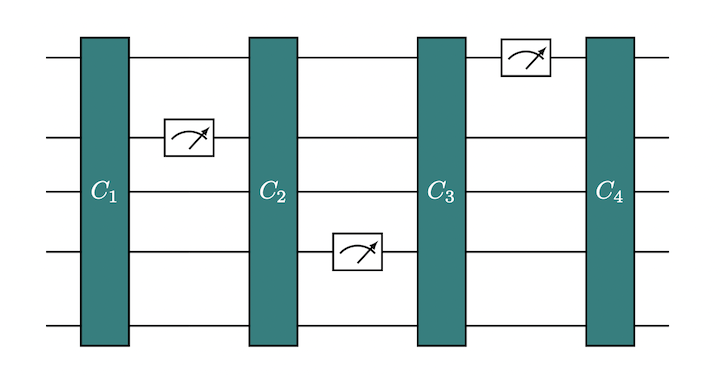
Above, the set up to construct a measurement-doped Clifford circuits. Projective measurments, in magic basis, is interleaved with global Clifford circuits that spread the magic throughout the system.